Einsteigerguide: Was versteht man unter Diffraction von Licht?

Wenn wir in klassischer Weise an Licht denken, assoziieren wir damit häufig gerade Linien, aber wenn Lichtquellen in der Nähe einer Barriere vorbeikommen, neigen sie dazu, sich um diese Barriere zu biegen und sich auszubreiten. Die Diffraction von Licht tritt auf, wenn eine Lichtwelle durch eine Ecke oder durch eine Öffnung oder einen Schlitz strömt, die physikalisch etwa so groß oder sogar kleiner als die Wellenlänge dieses Lichts ist.

Eine sehr einfache Demonstration der Diffraction kann durchgeführt werden, indem man die Hand vor eine Lichtquelle erhält und zwei Finger langsam schließt, während man das zwischen ihnen übertragene Licht beobachtet. Wenn sich die Finger einander nähern und sich sehr nahe kommen, beginnt man eine Reihe von dunklen Linien parallel zu den Fingern zu sehen. Die parallelen Linien sind eigentlich Diffraction-Muster. Dieses Phänomen kann auch auftreten, wenn Licht um Partikel „gebogen“ wird, die in der Größenordnung der Wellenlänge des Lichts liegen. Ein gutes Beispiel dafür ist die Diffraction des Sonnenlichts durch Wolken, die wir oft als Silberstreifen bezeichnen, wie oben in der Abbildung mit einem schönen Sonnenuntergang über dem Meer.

In Wolken können wir oft Pastelltöne von Blau, Pink, Lila und Grün beobachten, die entstehen, wenn Licht von Wassertropfen in den Wolken abgelenkt wird. Die Höhe der Diffraction hängt von der Wellenlänge des Lichts ab, wobei kürzere Wellenlängen in einem größeren Winkel gebeugt werden als längere (blaues und violettes Licht werden in einem höheren Winkel gebeugt als rotes Licht). Wenn eine Lichtwelle, die durch die Atmosphäre wandert, auf einen Wassertropfen trifft, wird sie zuerst an der water:air Schnittstelle gebrochen, dann wird sie reflektiert, wenn sie wieder auf die Schnittstelle trifft. Der Strahl, der sich noch immer im Wassertropfen bewegt, wird wieder gebrochen, als dieser zum dritten Mal auf die Schnittstelle trifft. Diese letzte Interaktion mit der Schnittstelle bricht das Licht zurück in die Atmosphäre, aber sie bricht auch einen Teil des Lichts ab. Dieses Diffraction-Element führt zu einem Phänomen, das als Cellinis Halo (auch Heiligenschein-Effekt genannt) bekannt ist, bei dem ein heller Lichtring den Schatten des Kopfes des Betrachters umgibt.

Die Begriffe Diffraction und Scattering werden oft synonym verwendet und gelten als fast gleichbedeutend. Diffraction beschreibt einen speziellen Fall des Licht-Scatterings, bei dem ein Objekt mit regelmäßig wiederkehrenden Merkmalen (z.B. ein Diffraction-Gitter) eine geordnete Diffraction des Lichts in einem Diffraction-Muster erzeugt. In der realen Welt sind die meisten Objekte sehr komplex in der Form und sollten als aus vielen einzelnen Diffraction-Merkmalen zusammengesetzt betrachtet werden, die zusammen ein zufälliges Licht-Scattering erzeugen können.

Eines der klassischen und grundlegendsten Konzepte der Diffraction ist das optische Diffraction-Experiment mit einem Spalt, das erstmals im frühen 19. Jahrhundert durchgeführt wurde. Wenn sich eine Lichtwelle durch einen Spalt (oder eine Öffnung) ausbreitet, hängt das Ergebnis von der physikalischen Größe der Öffnung in Bezug auf die Wellenlänge des einfallenden Strahls ab. Dies ist in der unteren Abbildung dargestellt, wobei davon ausgegangen wird, dass eine kohärente, monochromatische Welle, die von der Punktquelle S ausgestrahlt wird, ähnlich wie Licht, das von einem Laser erzeugt wird, durch die Öffnung d geht und gebeugt wird, wobei der primäre einfallende Lichtstrahl an Punkt P landet und die ersten sekundären Maxima an Punkt Q auftreten.

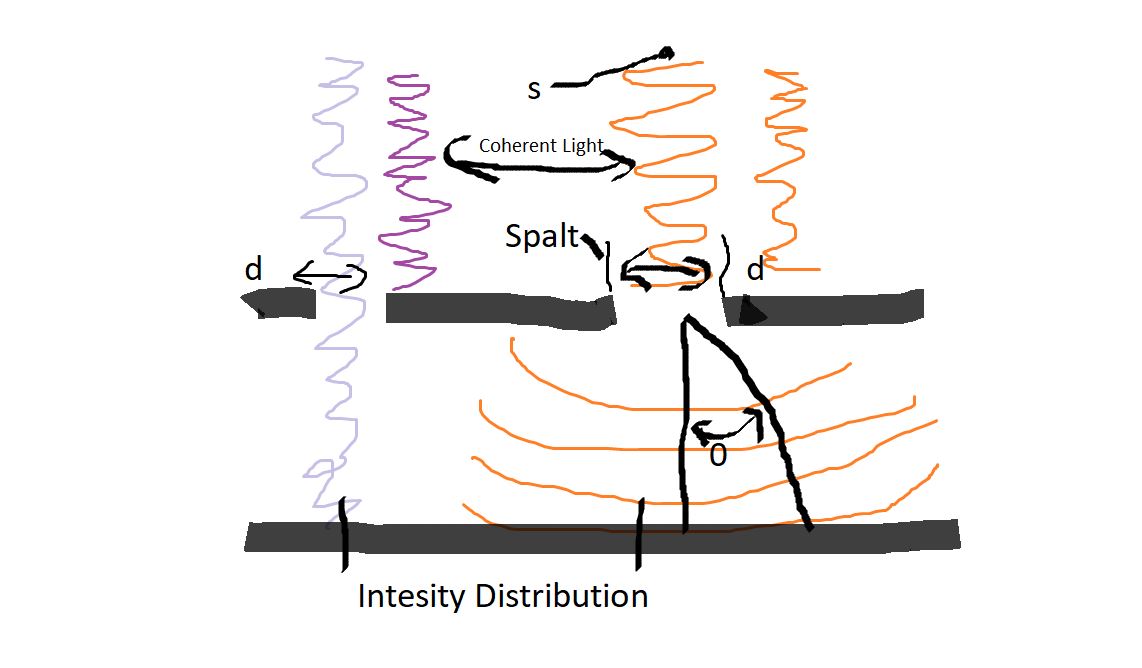
Wie auf der linken Seize der Abbildung zu sehen ist, wandert die Welle, wenn die Wellenlänge (λ) viel kleiner als die Aperture-Breite (d) ist, einfach geradlinig weiter, genau wie wenn es ein Partikel wäre oder keine Aperture vorhanden wäre. Wenn die Wellenlänge jedoch die Größe der Öffnung überschreitet, erleben wir eine Diffraction des Lichts nach der Gleichung:

sin0 = λ / d

Dabei ist θ der Winkel zwischen der einfallenden zentralen Ausbreitungsrichtung und dem ersten Minimum des Diffraction-Musters. Das Experiment erzeugt ein helles Zentralmaximum, das auf beiden Seiten von sekundären Maxima flankiert wird, wobei die Intensität jedes nachfolgenden sekundären Maximums mit zunehmenden Abstand vom Zentrum abnimmt. Die folgende Abbildung veranschaulicht diesen Punkt mit einem Diagramm aus Strahlintensität und Diffraction-Radius. Beachten Sie, dass sich die zwischen den sekundären Maxima auftretenden Minima in Vielfachen von π befinden.

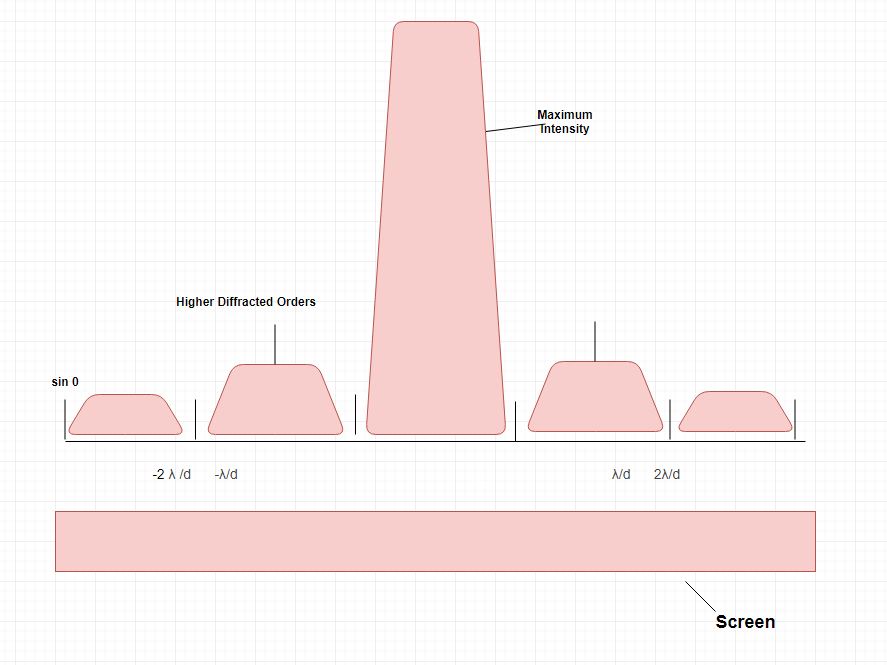
Dieses Experiment wurde erstmals von Augustin Fresnel erklärt, der zusammen mit Thomas Young wichtige Beweise dafür lieferte, dass sich Licht in Wellen bewegt. Aus den oberen Abbildungen sehen wir, wie ein kohärentes, monochromatisches Licht, das emittiert wird, durch die Öffnung d gebeugt wird. Fresnel ging davon aus, dass die Amplitude der Maxima erster Ordnung am Punkt Q durch die folgende Gleichung gegeben wäre:

dεQ = α(A/r)f(χ)d

wobei A die Amplitude der einfallenden Welle, r der Abstand zwischen d und Q ist und f (χ) eine Funktion von χ ist, einem von Fresnel eingeführten sogenannten Inclination-Faktor.

Licht Diffraction spielt eine entscheidende Rolle bei der Begrenzung des Auflösungsvermögens eines optischen Instruments (z.B. Kameras, Ferngläser, Teleskope, Mikroskope und das Auge). Das Auflösungsvermögen ist die Fähigkeit des optischen Instruments, getrennte Bilder von zwei benachbarten Punkten zu erzeugen. Dies wird oft durch die Qualität der Linsen und Spiegel im Gerät sowie die Eigenschaften des umgebenden Mediums (meistens Luft) bestimmt. Die wellenartige Natur des Lichts zwingt die ultimative Grenze des Auflösungsvermögens aller optischen Instrumente.

Unsere Diskussionen über Diffraction haben einen Spalt als Öffnung verwendet, durch den das Licht gebeugt wird. Alle optischen Instrumente haben jedoch kreisförmige Öffnungen, z.B. die Pupille eines Auges oder die kreisförmige Membran und Linsen eines Mikroskops. Kreisförmige Öffnungen erzeugen Diffraction-Muster, die denen der oben beschriebenen ähneln, mit der Ausnahme, dass das Muster natürlich eine kreisförmige Symmetrie aufweist. Die mathematische Analyse der Diffraction-Muster, die durch eine kreisförmige Öffnung erzeugt werden, wird durch die folgende Gleichung beschrieben:

sinθ(1) = 1.22(λ/d)

wobei θ(1) die Winkelposition des Diffraction-Minimums erster Ordnung (des ersten dunklen Rings), λ die Wellenlänge des einfallenden Lichts, d der Durchmesser der Öffnung und 1,22 eine Konstante ist. Unter den meisten Umständen ist der Winkel θ(1) sehr klein, so dass die Approximation an den Sinus und die Tangente des Winkels fast gleich groß sind:

θ(1) ≅ 1.22(λ/d)

Aus diesen Gleichungen wird deutlich, dass das zentrale Maximum direkt proportional zu λ/d ist, so dass dieses Maximum für längere Wellenlängen und für kleinere Aperturen besser verteilt ist. Die sekundäre Mimik der Diffraction setzt der nützlichen Vergrößerung von Objektiven in der optischen Mikroskopie aufgrund der inhärenten Diffraction des Lichts durch diese Linsen eine Grenze. Unabhängig davon wie perfekt das Objektiv auch sein mag, das Bild einer punktförmigen Lichtquelle, die von dem Objektiv erzeugt wird, wird von sekundären und höherwertigen Maxima begleitet. Dies konnte nur beseitigt werden, wenn das Objektiv einen unendlichen Durchmesser hatte. Zwei Objekte, die durch einen Abstand von weniger als θ(1) getrennt sind, können nicht aufgelöst werden, unabhängig davon, wie hoch die Vergrößerungskraft ist. Während diese Gleichungen für das Bild einer punktförmigen Lichtquelle in unendlicher Entfernung von der Blende abgeleitet wurden, ist es eine angemessene Approximation an das Auflösungsvermögen eines Mikroskops, wenn d durch den Durchmesser der Objektlinse ersetzt wird.

Wenn also zwei Objekte in einem Abstand voneinander und in einem Abstand L von einem Beobachter liegen, ist der Winkel (ausgedrückt in Radians) zwischen ihnen:

θ = D / L

was uns in die Lage versetzt, die letzten beiden Gleichungen zu verdichten, um Folgendes zu liefern:

D(0) = 1.22(λL/d)

wobei D(0) der minimale Trennungsabstand zwischen den Objekten ist, der es ermöglicht, sie zu lösen. Mit dieser Gleichung kann das menschliche Auge Objekte, die durch einen Abstand von 0,056 Millimetern voneinander getrennt sind, auflösen, jedoch sind die Photorezeptoren in der Netzhaut nicht ganz nah genug beieinander, um diesen Auslösungsgrad zu ermöglichen, und 0,1 Millimeter sind unter normalen Umständen eine realistischere Zahl.

Das Auflösungsvermögen von optischen Mikroskopen wird durch eine Reihe von Faktoren bestimmt, einschließlich der genannten, aber unter den idealsten Umständen liegt diese Zahl bei etwa 0,2 Mikrometern. Diese Zahl muss die optische Ausrichtung des Mikroskops, die Qualität der Linsen sowie die vorherrschenden Wellenlängen des Lichts zur Abbildung der Probe berücksichtigen. Obwohl es oft nicht notwendig ist, das genaue Auflösungsvermögens jedes Objektivs zu berechnen (und in den meisten Fällen Zeitverschwendung wäre), ist es wichtig, die Fähigkeiten der Mikroskop-Objektive zu verstehen, wie sie in der realen Welt gelten.

Wir hoffen, dass wir Ihnen einen ersten kleinen Überblick über diese Thematik bieten konnten. Wenn Sie noch Fragen oder Anregungen haben sollten, hinterlassen Sie uns unten einen Kommentar.

Vielen Dank für Ihren Besuch.