WebGL Grundlagen 7 – einfache und ambiente Beleuchtung.

Herzlich Willkommen zu unserem siebten Grundlagenteil zu WebGL. In diesem Beitrag werden wir thematisieren, wie Sie einfache Beleuchtung zu ihrer WebGL-Seite hinzufügen. Dies erfordert etwas mehr Arbeit in WebGL als in OpenGL, aber hoffentlich ist alles ziemlich einfach zu verstehen.

So wird das Ergebnis nach der entsprechenden Umsetzung aussehen:

Sie sehen einen langsam drehenden Würfel, dessen Beleuchtung von einem Punkt nach vorne leicht über und nach rechts zu kommen scheint.

Sie können das Kontrollkästchen unter der Leinwand verwenden, um die Beleuchtung auszuschalten und einzuschalten, so dass Sie sehen können, welchen Effekt Sie hat. Sie können auch die Farbe des gerichteten und des Umgebungslichts und die Richtung des gerichteten Lichts ändern. Testen Sie es aus. Besonders viel Freude bereitet es, Spezialeffekte mit gerichteten RGB-Beleuchtungswerten mit mehr als nur eine Alternative auszuprobieren. Außerdem können Sie auch die Cursortasten benutzen, um die Box schneller und langsamer drehen zu lassen. Zum Vergrößern und Verkleinern können Sie die Page Up und Page Down-Tasten verwenden. Wir verwenden hier den besten Texturfilter, so dass die F-Taste nichts mehr macht.

Es existieren zwei verschiedene Möglichkeiten, den Code für dieses Beispiel zu erhalten. In den Browsereinstellungen mit „View Source“, während Sie sich die Live-Version ansehen oder wenn Sie GitHub verwenden, können Sie es aus dem Repository kopieren. Unabhängig davon für welchen Weg Sie sich entscheiden, sollten Sie ihren bevorzugten Texteditor herunterladen und Sie den Code genau ansehen.

Bevor wir uns mit den Details der Beleuchtung in WebGL widmen, müssen Sie zunächst eine schlechte Nachricht verdauen. WebGL hat absolut keine eingebaute Unterstützung für Beleuchtungen. Im Gegensatz zu OpenGL, bei dem Sie mindestens 8 Lichtquellen angeben und alle bearbeiten können, müssen Sie mit WebGL alles selber machen. Aber die Beleuchtung ist eigentlich ziemlich einfach, wenn man Sie einmal verstanden hat. Wenn Sie unsere bisherigen Ausführungen zu Shadern erfolgreich durchgearbeitet haben, werden Sie mit der Beleuchtung voraussichtlich keinerlei Probleme haben. Sollten Sie als Anfänger ihre eigenen einfachen Lichter programmieren, ist es viel einfacher, den Code zu verstehen als wenn Sie diesen selber schreiben müssen und über fortgeschrittene Kenntnisse verfügen. Schließlich ist die OpenGL-Beleuchtung zu einfach für realistische Szenen, da Sie z.B. keinen Schatten behandelt und bei gekrümmten Flächen kann Sie ziemlich raue Effekte erzeugen, so dass alles was über einfache Szenen hinausgeht manuell programmiert werden muss.

Lassen Sie uns damit beginnen darüber nachzudenken, was wir von der Beleuchtung erwarten. Ziel ist es eine Vielzahl von Lichtquellen innerhalb der Szene simulieren zu können. Diese Quellen müssen nicht selbst sichtbar sein, aber Sie müssen die 3D-Objekte realistisch beleuchten, so dass die dem Licht zugewandte Seite des Objekts hell und die vom Licht entfernte Seite dunkel erscheint. Oder anders ausgedrückt: Wir wollen in der Lage sein eine Reihe von Lichtquellen zu spezifizieren, dann wollen wir für jeden Teil unserer 3D-Szene herausfinden, wie sich alle Lichter auf Sie auswirken. Mittlerweile bin ich mir sicher, dass Sie WebGL gut genug kennen um zu erkennen, dass es sich dabei um Dinge mit Shadern handeln wird. Wir werden Vertex-Shader schreiben, welche die Beleuchtung handhaben. Wir werden die Auswirkungen des Lichts für jeden Scheitelpunkt analysieren und dabei die Erkenntnisse nutzen, um die Farbe entsprechend anzupassen. Wir werden es im Folgenden nur für eine Leuchte tun.

Eine Randbemerkung: Da wir die Beleuchtung auf Basis von Per-Vertex ausarbeiten, werden die Effekte des Lichts auf die Pixel, die zwischen den Ecken liegen, durch die übliche lineare Interpolation berechnet. Das bedeutet, dass die Zwischenräume zwischen den Eckpunkten so beleuchtet werden, als wären sie flach. Das ist für uns sehr praktisch, weil wir einen Würfel zeichnen wollen. Für gekrümmte Flächen, bei denen Sie die Beleuchtungseffekte für jedes Pixel unabhängig voneinander berechnen möchten, können Sie eine Technik verwenden, die als per-Fragment Lighting bezeichnet wird. Das per-Fragment Lighting ist bekannt dafür deutlich bessere Ergebnisse zu liefern. Wir werden uns auch intensiver mit der fragmentierten Beleuchtung befassen. Was wir hier tun werden, nennt man logischerweise per-Vertex-Beleuchtung.

Weiter zum nächsten Schritt: Was machen wir, wenn unsere Aufgabe darin besteht, einen Vertex-Shader zu schreiben, welche in der Lage ist herauszufinden, wie eine einzelne Lichtquelle die Farbe am Vertex beeinflusst? Ein guter Ausgangspunkt ist das Phong Reflection Model. Ich fand dies am einfachsten zu verstehen, indem ich mit den folgenden Punkten begann:

Während es in der realen Welt nur eine Art von Licht gibt, ist es in der Grafik möglich, dass es zwei Arten von Licht gibt:

1. Licht, welches aus einer bestimmten Richtung kommt und nur Objekte beleuchtet, die in die Richtung zeigen aus der das Licht kommt. Wir nennen das Richtungslicht.
2. Licht, welches von überall herkommt und alles gleichmäßig beleuchtet unabhängig davon in welche Richtung es zeigt. Dies wird als Umgebungslicht bezeichnet.

Wenn Licht auf eine Oberfläche trifft löst es sich auf zwei verschiedene Arten ab:

1. Diffus, d.h. unabhängig vom Winkel. Das Licht trifft auf die Oberfläche und wird gleichmäßig in alle Richtungen abgeprallt. Unabhängig davon aus welchem Blickwinkel man es betrachtet, die Helligkeit des reflektierenden Lichts wird ganz von dem Winkel bestimmt, in dem das Licht auf die Oberfläche trifft – je steiler der Einfallswinkel, desto dunkler die Reflexion. Diese diffuse Reflexion ist es, woran wir normalerweise denken, wenn wir an ein beleuchtetes Objekt denken.
2. Specularly, d.h. spiegelverkehrt. Der Teil des Lichts, welcher auf diese Weise reflektiert wird, prallt im gleichen Winkel von der Oberfläche ab. In diesem Fall hängt die Helligkeit des vom Material reflektierten Lichts davon ab, ob sich ihre Augen zufällig in der Linie befinden auf der das Licht abgeprahlt wurde – d.h. es hängt nicht nur vom Winkel ab, in dem das Licht auf die Oberfläche trifft, sondern auch vom Winkel zwischen ihrer Sichtlinie und der Oberfläche. Diese Spiegelreflexion ist es, die auf Objekten „Schimmer“ und „Glanzlichter“ hervorruft und die Spiegelreflexion kann natürlich von Material zu Material variieren. Ein Beispiel: ungeschliffenes Holz hat wahrscheinlich nur sehr wenig Spiegelreflexion zbd hochglanzpoliertes Metall hat ziemlich viel.

Das Phong-Modell fügt diesem Vier-Stufen-System eine weitere Wendung hinzu, indem es sagt, dass alle Leuchten zwei Eigenschaften haben:

1. Die RGB-Werte für das von ihnen erzeugte diffuse Licht.
2. Die RGB-Werte für das von ihnen erzeugte spielerische Licht.

…und dass alle Materialien vier haben:

1. Die RGB-Werte für das von ihnen reflektierte Umgebungslicht.
2. Die RGB-Werte für das diffuse Licht, welches Sie reflektieren.
3. Die RGB-Werte für das spiegelnde Licht, welches Sie reflektieren.
4. Der Glanz des Objekts, welches die Details der Spiegelreflexion bestimmt.

Für jeden Punkt der Szene ist die Farbe eine Kombination aus der Farbe des auf Sie einfallenden Lichts, den eigenen Farben des Materials und den Lichteffekten. Um die Beleuchtung in einer Szene nach dem Phong-Modell vollständig zu spezifizieren, benötigen wir also zwei Eigenschaften pro Licht und vier pro Punkt auf der Oberfläche unseres Objekts. Das Umgebungslicht ist naturgemäß nicht an ein bestimmtes Licht gebunden, aber wir brauchen eine Möglichkeit, die Menge des Umgebungslichts für die Szene als Ganzes zu speichern. Manchmal kann es am einfachsten sein, für jede Lichtquelle nur einen Umgebungspegel anzugeben und diese dann zu einem einzigen Begriff zusammenzufassen.

Sobald wir alle diese Informationen haben, können wir Farben herausarbeiten, die auf der umgehenden, gerichteten und spiegelnden Reflexion des Lichtes an jedem Punkt bezogen werden und Sie dann zusammenaddieren, um die Gesamtfarbe auszuarbeiten. Hier ist ein hervorragendes Diagramm auf Wikipedia, welche die Funktionsweise eingehend erläutert. Alles, was unser Shader tun muss, ist es für jeden Scheitelpunkt die Beiträge zu den roten, grünen und blauen Farben des Scheitelpunktes für die ambiente, diffuse und spiegelnde Beleuchtung auszuarbeiten, und Sie zu verwenden, um die RGB-Komponenten der Farbe zu gewichten, Sie alle zusammen zu addieren und das Ergebnis auszugeben.

Auch in diesem Beitrag werden wir versuchen die Dinge möglichst einfach zu halten. Wir werden nur diffuses und ambientes Licht in Betracht ziehen und die Spiegelung ignorieren. Wir verwenden den texturierten Würfel aus dem letzten Beitrag und gehen davon aus, dass die Farben in der Textur die Werte sind, die sowohl für die diffuse als auch für die Umgebungsreflexion verwendet werden. Und schließlich betrachten wir nur eine einfache Art der diffusen Beleuchtung – die einfachste Art der gerichteten Beleuchtung. Es lohnt sich diesen Sachverhalt mit einem Diagramm zu veranschaulichen:

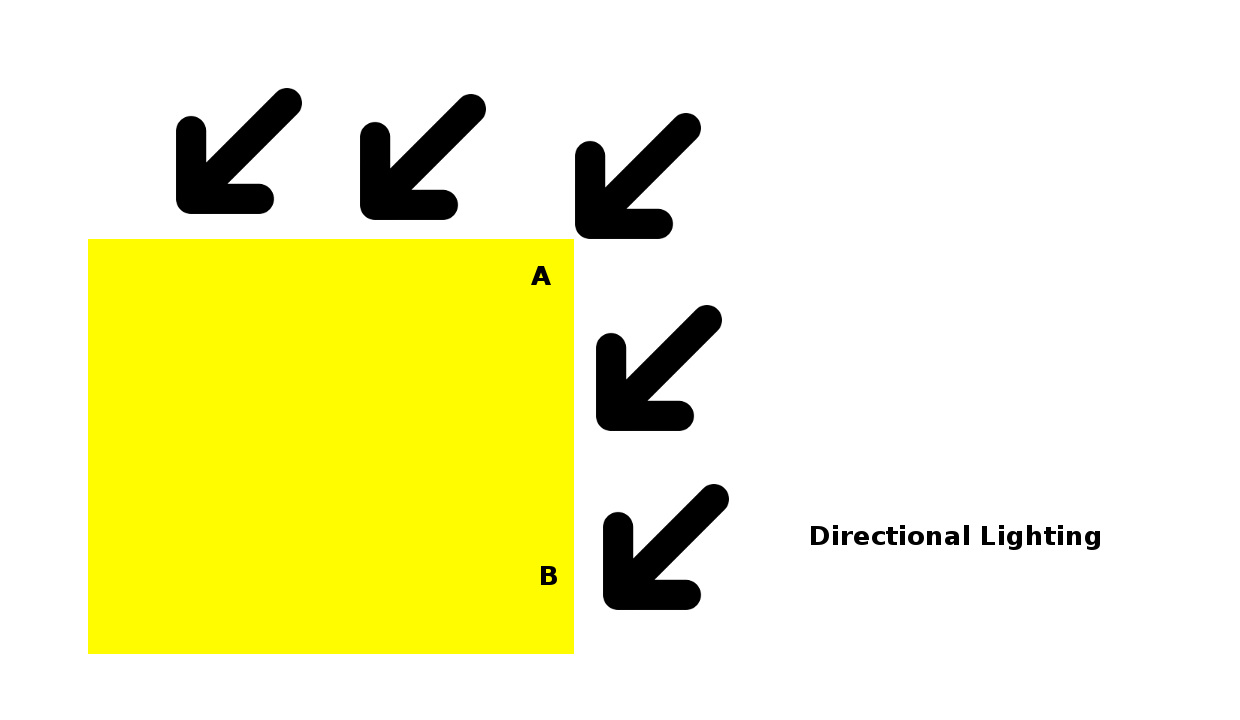
Licht welches aus einer Richtung auf eine Fläche trifft, kann zwei Arten von Licht sein: einfaches, gerichtetes Licht, das in die gleiche Richtung über die gesamte Szene verteilt ist und Licht, das von einem einzigen Punkt innerhalb der Szene kommt.

Bei der einfachen gerichteten Beleuchtung ist der Winkel, in dem das Licht auf die Scheitelpunkte einer trifft – an den Punkten A und B des Diagramms – immer gleich. Denken Sie an das Licht der Sonne, alle Strahlen sind parallel.

Wenn stattdessen das Licht von einem Punkt innerhalb der Szene kommt, wird der Winkel der durch das Licht erzeugt wird an jedem Scheitelpunkt anders sein. An Punkt A in diesem Diagramm beträgt der Winkel etwa 45 Grad, während er an Punkt B in etwa 90 Grad zur Oberfläche beträgt.

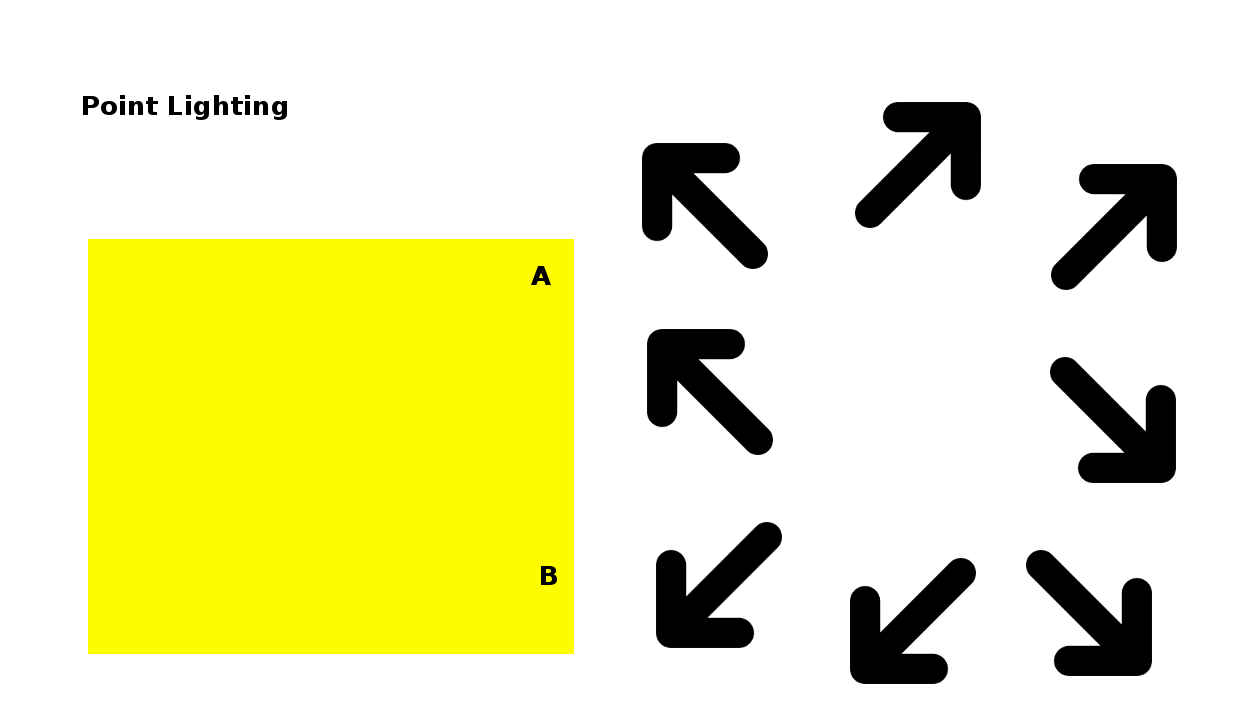
Das bedeutet, dass wir bei der Punktbeleuchtung für jeden Scheitelpunkt die Richtung bestimmen müssen, aus der das Licht kommt, während wir bei der gerichteten Beleuchtung nur einen Wert für die gerichtete Lichtquelle benötigen. Dies macht die Punktberechnung ein wenig schwieriger, so dass in diesem Beitrag lediglich eine einfache gerichtete Beleuchtung verwendet wird und die Punktebeleuchtung später kommt.

So, jetzt haben wir das Problem noch ein wenig verfeinert. Wir wissen, dass das gesamte Licht in unserer Szene in eine bestimmte Richtung kommt und diese Richtung wird sich nicht von Scheitelpunkt zu Scheitelpunkt ändern. Das bedeutet, dass wir es in eine einheitliche Variable stellen können und der Shader kann es aufnehmen. Wir wissen auch, dass der Effekt, den das Licht an jedem Scheitelpunkt hat durch den Winkel bestimmt wird, also müssen wir die Ausrichtung der Oberfläche irgendwie darstellen. Der beste Weg in der 3D-Geometrie besteht darin, den Normalvektor zur Oberfläche am Scheitelpunkt anzugeben. Dies erlaubt es uns, die Richtung in der die Oberfläche ausgerichtet ist, als eine Menge von drei Zahlen anzugeben.

Sobald wir das Normal haben ist ein letztes Stück erforderlich, bevor wir unseren Shader schreiben können. Wenn man den normalen Vektor einer Oberfläche an einem Scheitelpunkt und den Vektor der die Richtung beschreibt aus der das Licht kommt betrachtet, müssen wir herausfinden, wie viel Licht die Oberfläche diffus reflektiert. Dies stellt sich als proportional zum Cosinus des Winkels zwischen diesen beiden Vektoren heraus. Wenn der normale Vektor Null Grad ist, dann können wir daraus schließen, dass es das gesamte Licht reflektiert. Wenn der Winkel des Lichts zur Normal 90 Grad beträgt wird nichts reflektiert. Und für alles dazwischen folgt er der Kurve des Cosinus.

Für uns bequem ist eine triviale Berechnung den Cosinus des Winkels zwischen zwei Vektoren zu berechnen, wenn beide eine Länge von einem haben. Dies geschieht, indem man ihr Punktprodukt nimmt. Und noch bequemer ist es, dass Dot-Produkte mit Hilfe der logisch benannten Dot-Funktion im Shader eingebaut werden.

Puh! Das war eine Menge Theorie, mit dem wir begonnen haben – aber nun wissen wir, das alles, was wir tun müssen, um eine einfache, gerichtete Beleuchtung zum Laufen zu bringen Folgendes ist:

• Behalten Sie einen Satz normaler Vektoren, einen für jeden Scheitelpunkt.
• Behalten Sie einen Richtungsvektor für das Licht.
• Berechnen Sie im Vertex-Shader das Punktprodukt aus dem Normalwert des Vertex und dem Beleuchtungsvektor, gewichten Sie die Farben entsprechend und fügen Sie eine Komponente für die Umgebungsbeleuchtung hinzu.

Lassen Sie uns einen Blick auf den Code werfen. Wir fangen unten an und arbeiten uns nach oben hoch. Offensichtlich unterscheidet sich das HTML für diesen Beitrag von dem letzten, weil wir alle zusätzlichen Eingabefelder haben, aber ich werde Sie nicht mit den Details langweilen… gehen wir zum JavaScript, wo unsere erste Anlaufstelle die initBuffers-Funktion ist. An der Stelle nach dem Code, der den Puffer mit den Vertexpositionen erzeugt und vor dem Code, der das Gleiche mit den Texturkoordinaten tut, sehen Sie einen Code um die Normals einzurichten. Das sollte mittlerweile recht vertraut aussehen:

Ganz einfach. Die nächste Änderung ist etwas weiter unten in drawScene und ist nur der Code welcher benötigt wird, um diesen Puffer an das entsprechende Shader-Attribut zu binden:

Hier haben wir den Code aus Beitrag 6 entfernt, welcher uns es erlaubt hatte, zwischen den Texturen zu wechseln, so dass wir nur eine Textur verwenden können:

Das nächste Snippet ist ein wenig komplizierter. Zuerst schauen wir, ob das Kontrollkästchen „Beleuchtung“ aktiviert ist und stellen eine Uniform für unsere Shader ein, die ihnen mitteilt, ob Sie es ist oder nicht:

Als nächstes, wenn die Beleuchtung aktiviert ist, sehen wir die Rot-, Grün- und Blau-Werte für die Umgebungsbeleuchtung, wie Sie in den Eingabefeldern unten auf der Seite angegeben sind und schieben diese ebenfalls bis zu den Shadern hoch:

Als nächstes schieben wir die Richtung des Lichts nach oben:

Sie können sehen, dass wir den Lichtrichtungsvektor anpassen, bevor wir ihn an den Shader übergeben, indem wir das Modul vec3 verwenden – welches, wie das Modul mat4, das wir für unsere Model-View- und Projektionsmatrizen verwenden Teil von glMatrix ist. Die erste Einstellung vec3.normalize skaliert Sie nach oben oder unten, so dass ihre Länge eins ist. Sie werden sich daran erinnern, dass der Cosinus des Winkels zwischen zwei Vektoren gleich den Punktprodukt sein muss, damit Sie beide die Länge eins haben. Die definierten Normals hatten alle die richtigen Länge, aber da die Lichtrichtung vom Benutzer eingegeben wird, konvertieren wir diese. Die zweite Anpassung besteht darin den Vektor mit einem Skalar -1 zu multiplizieren, d.h. seine Richtung umzukehren. Das liegt daran, dass wir die Lichtrichtung in Bezug auf die Richtung des Lichtes festlegen, während die Berechnungen, die wir vorher besprochen haben, sich auf die Richtung beziehen aus der das Licht kommt. Sobald wir das getan haben, geben wir es an die Shader weiter, indem wir gl.uniform3fv verwenden, was ein Float32Array mit drei Elementen in eine Uniform bringt.

Der nächste Code-Bit ist einfacher. Es kopiert lediglich die Farbkomponenten des gerichteten Lichts bis hin zur entsprechenden Shader-Uniform:

Das sind alle Änderungen in drawScene. Wenn man nun zum Key-Handling-Code aufsteigt, so sieht man einfache Änderungen, um den Handler für die F-Taste zu entfernen, welche ignoriert werden kan. Die nächste interessante Änderung in der Funktion setMatrixUniforms, die Sie sich merken sollten, kopiert die Model-View und Projektionsmatrizen bis hin zu den Uniformen des Shaders. Wir haben vier Zeilen hinzugefügt, um eine neue Matrix zu kopieren, die auf dem Model-View basiert:

Wie man es von einer Matrix als Normal erwarten würde, wird es verwendet, um die Normals zu transformieren. Wir können Sie nicht auf die gleiche Weise transformieren, wie wir die Vertex-Positionen mit Hilfe der regulären Model-View-Matrix transformieren, weil Normals sowohl durch unsere Übersetzungen als auch durch unsere Rotationen konvertiert würden, so z.B. wenn wir die Rotation ignorieren und davon ausgehen, dass wir eine mvTranslate von (0, 0 ,0 , -5) generiert haben, würde die Normal von (0 ,0 ,0 ,1) zu (0, 0, -4) werden. Wir können das umgehen. Sie haben vielleicht bemerkt, dass wir in den Vertex-Shadern, wenn wir die 3-Element-Vertex-Positionen mit der 4×4-Modell-View-Matrix multiplizieren, um die beiden kompatibel zu machen, die Vertex-Positionen auf vier Elemente erweitern, indem wir eine zusätzliche 1 am Ende hinzufügen. Diese 1 wird nicht nur benötigt um Dinge auszufüllen, sondern auch um die Multiplikation dazu zu bringen, Übersetzungen sowie Rotationen und andere Transformationen anzuwenden. Darüber hinaus werden durch das Hinzufügen einer 0 anstelle einer 1 die Multiplikation dazu bringen könnten die Übersetzungen zu ignorieren. Das würde für uns im Moment sehr gut funktionieren, aber leider nicht für alle Fälle in denen unsere Model-View-Matrix verschiedene Transformationen enthielt insbesondere Skalierung und Shearing. Wenn wir zum Beispiel eine Model-View-Matrix hätten, die die Größe der Objekte verdoppelt, die wir zeichnen, würden ihre Normals auch doppelt so lang werden, sogar mit einer nachlaufenden Null – was zu ernsten Problemen mit der Beleuchtung führen würde. Um nicht in schlechte Gewohnheiten abzurutschen machen wir es richtig.
Der korrekte Weg, um die Normals in die richtige Richtung zu bringen ist die Verwendung der transponierten Inverse des oben linken 3×3 Teils der Model-View-Matrix.

Wie auch immer, sobald wir diese Matrix berechnet und ausgeführt haben, word Sie in die Shader-Uniforms gelegt, genau wir die anderen Matrizen.
Wenn man sich von dort aus durch den Code bewegt, gibt es ein paar triviale Änderungen am Textur-Loadcode, damit es nur eine Mipmapped-Textur lädt. Zudem fügen wir noch ein paar neue Codes in initShaders hinzu, um das Attribut vertexNormalAttribute auf dem Programm zu initialisieren, so dass drawScene es benutzen kann. Wir werden diese Aspekte im Folgenden vernächlässigen und direkt zu den Shadern übergehen.

Der Fragment-Shader ist einfacher, also schauen wir es uns erst einmal an:

Wir extrahieren hier die Farbe aus der Textur genauso wie im sechsten Beitrag, aber bevor wir Sie zurückgeben, passen wir ihre RGB-Werte durch eine Variable mit der Bezeichnung vLightWeighting an. VlightWeighting ist ein 3-Element-Vektor und enthält Korrekturfarben für Rot, Grün und Blau, die aus der Beleuchtung durch den Vertex-Shader berechnet werden.

Im Folgenden schauen wir den Vertex-Shader-Code etwas genauer an.

Das neue Attribut, aVertexNormal, enthält natürlich die Vertex-Normals, die wir in initBuffers spezifizieren und an den Shader in drawScene übergeben. UNMatrix ist unsere normale Matrix, uUseLighting ist die einheitliche Angabe, ob die Beleuchtung eingschaltet ist und uAmbientColor, uDirectionalColor und uLightingColor sind die Werte, die der Nutzer in den Eingabefeldern der Website angibt.

Vor dem Hintergrund der Mathematik, die wir oben durchlaufen haben, sollte der eigentliche body des Codes recht einfach zu verstehen sein. Die Hauptausgabe des Shaders ist die Variable vLightWeighting, die wir gerade gesehen haben, um die Farbe des Bildes im Fragment-Shader anzupassen. Wenn die Beleuchtung ausgeschaltet ist, verwenden wir nur den Standardwert (1, 1, 1, 1), d.h. die Farben sollten nicht verändert werden. Wenn die Beleuchtung eingeschaltet ist, berechnen wir die Orientierung der Normals, indem wir die normale Matrix anwenden. Anschließend nehmen wir das Punktprodukt der Normals und die Beleuchtungsrichtung, um eine Zahl zu erhalten, wieviel Licht reflektiert wird. Wir können dann für den Fragment-Shader eine abschließende Light-Weighting-Bewertung ausarbeiten, indem wir die Farbkomponenten des gerichteten Lichts mit dieser Gewichtung multiplizieren und dann die Farbe des Umgebungslichts hinzufügen. Nun hat der Fragment-Shader alles was er braucht. Wir sind fertig.

Nun haben Sie ein solides Wissen darüber, wie Beleuchtung in Grafiksystemen wie WebGL funktioniert und sollten die Details darüber kennen, wie Sie die beiden einfachsten Formen der Beleuchtung, ambient und directional, implementieren können.